Salut les Inphinautes,
Aujourd’hui je vous propose, pour ce premier portrait, de parler de la plus grande mathématicienne du XXième siècle et, ce, selon bon nombre de ses confrères et consœurs ! Elle sera pour toujours un exemple de génie, d’humilité, de sacrifice, de bienveillance, de résilience et de quête du savoir.
Plus qu’une grande mathématicienne, Emmy Noether est une des plus grandes figures scientifiques du XXième siècle, dont l’histoire résonne encore – parfois bien tristement – aujourd’hui.
Une jeunesse en Bavière
Amalie Emmy Noether – de son nom complet – naît à Erlangen, près de Nuremberg, le 23 mars 1882. Elle est la fille du mathématicien Max Noether et d’Ida Amalia Kaufmann. Elle est également la grande sœur de Gustav Robert, d’Alfred – qui sera chimiste – et de Fritz – qui deviendra également mathématicien.
Elle fait une scolarité tout à fait correcte, et montre des aptitudes particulières pour la résolution d’énigmes et de problèmes logiques. Fillette de la fin du XIXe siècle, elle va recevoir, en plus de sa scolarité, des leçons de tâches domestiques, de piano et de danse… mais rien de tout cela ne va particulièrement la passionner. Comme elle a de bons résultats en français et en anglais, elle va passer un examen pour enseigner ces matières et elle l’obtiendra haut la main.
Mais ça non plus, ça ne la passionne pas…
Les mathématiques pour unique but
Ce qui passionne Emmy, vous l’aurez deviné, ce sont les maths. Et ce qu’elle veut, c’est entrer à l’université d’Erlangen où enseigne son père.
Nous sommes en 1900. l’année où les femmes sont autorisées à suivre des cours… ou plutôt… elles ne s’en voient pas interdire l’accès. Elles sont admises, en quelques sorte, en auditrices libres. Emmy va donc pouvoir assister aux cours sans vraiment voir son travail reconnu et devra demander une dérogation à chaque professeur pour pouvoir passer un examen.
Elle acceptera toutes ces conditions car son unique objectif sera la connaissance.
Premier séjour à Göttingen

En 1903, elle passe donc son examen à Nuremberg. Ce sera pour elle un passeport pour une des plus prestigieuses universités allemandes de cette époque : l’Université de Göttingen.
Gauss, Riemann, Minkowski, Hilbert… tous les plus grands mathématiciens allemands y sont passés !
Elle va y passer un premier semestre et suivre justement les cours de Minkowski et Hilbert, mais aussi ceux de l’astronome Karl Schwartzschild – qui fût le premier à théoriser l’existence des trous noirs.
Après ces quelques mois passés à Göttingen, Emmy rentre à Erlangen pour y découvrir – enfin – une bonne surprise :
Les femmes à l’université… ou presque
Nous sommes en 1904 et les lois de restriction des droits des femmes sont levées. Les femmes peuvent alors pleinement étudier à l’université et Emmy entre donc officiellement à l’université d’Erlangen le 24 octobre 1904 !
Elle va alors y préparer une thèse portant sur les invariants algébriques sous la direction de Paul Gordan. Elle obtiendra son doctorat en 1907, ce qui lui permettra alors d’enseigner à l’université d’Erlangen… à titre bénévole.
Elle acceptera de nouveau l’inacceptable au nom de la connaissance et de la transmission de celle-ci, et sera aidée financièrement par sa famille.
Point mathématique facultatif : les invariants algébriques
Un invariant algébrique est un élément d’un ensemble qui ne change pas lorsqu’on applique une transformation à cet ensemble.
Prenons un exemple trivial mais parlant : un cercle est défini par son rayon, ici je l’appelle OA. On voit que si j’applique une rotation de -30° à mon cercle de centre O, le rayon reste le même : c’est un invariant, lié au fait que notre cercle soit parfaitement symétrique par rotation.
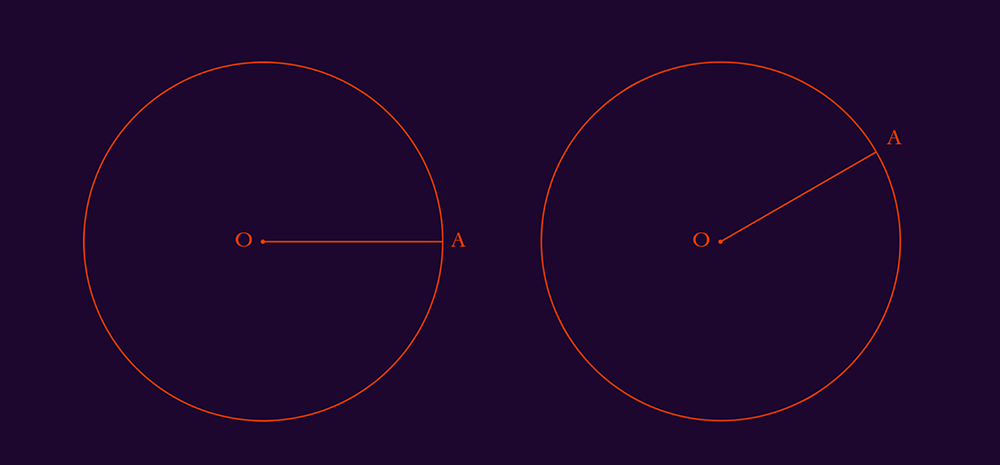
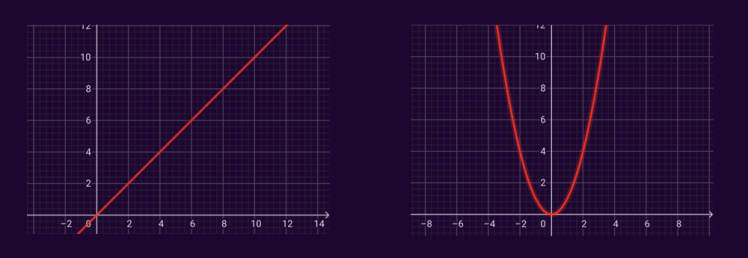
Deuxième exemple, pour le sport : imaginons une fonction, la plus simple possible, la fonction affine f(x)=x, qui pour chaque valeur de x, renvoie cette même valeur (à gauche) et appliquons une transformation qui consiste à renvoyer, pour chaque valeur de x, son carré. On obtient alors la fonction carrée (à droite), plus du tout linéaire, mais parabolique. On voit bien que la fonction a été changée. Et pourtant, pour les valeurs x=0 et x=1, la fonction renvoie également f(x) = 0 et f(x) = 1.
En effet 0 et 1 élevés au carré restent 0 et 1 ! Ces points n’ont donc pas bougé, ce sont des invariants algébriques.
Ces invariants vont permettre de simplifier des problèmes, car on pourra facilement identifier ce qui ne change pas au cours d’une transformation, même dans des cas bien plus complexes que ces deux exemples.
Retour à Göttingen
Faisons un saut en avant dans le temps : en 1915, Einstein publie sa théorie de la Relativité Générale. C’est une révolution dans le monde de la physique. David Hilbert va alors travailler sur certains aspects mathématiques de cette théorie qui le fascine, notamment sur une idée centrale : les invariants... Ça vous rappelle quelqu’un ?
Il se souvient en effet de la thèse d’Emmy Noether sur les invariants algébriques, et l’invite à Göttingen pour travailler le sujet à 4 mains.

C’est pendant ce travail qu’Emmy Noether va proposer un « monument de la pensée mathématique » – d’après Einstein lui même : son fameux Théorème.
Le Théorème de Noether
« À toute transformation infinitésimale qui laisse le lagrangien d’un système invariant à une dérivée temporelle totale près correspond une grandeur physique conservée.«
Voici l’énoncé mathématique du théorème, que l’on pourrait traduire plus simplement par : « Chaque symétrie et chaque invariance d’un système physique correspond à une loi de conservation ».
Prenons un exemple : si je lâche un objet d’une certaine hauteur, son énergie totale est donnée par la somme de son énergie cinétique et de son énergie potentielle. E(tot) = E(cin) + E(pot).
Au cours de la chute, l’énergie cinétique dépendant de la vitesse et l’énergie potentielle dépendant de la hauteur, ces grandeurs varient…
Mais elles varient en se compensant de telle façon que l’énergie totale reste invariante !
C’est la loi de conservation de l’énergie. Ce que le théorème de Noether nous apprend, c’est que cette conservation est liée à une symétrie temporelle.
Passons toutes ces symétries en revue :
– La symétrie temporelle, nous venons de le voir, implique la conservation de l’énergie.
– La symétrie spatiale implique la conservation de l’impulsion (p= masse x vitesse).
– La symétrie par rotation implique la conservation du moment angulaire (L= masse x vitesse x rayon)
Mais alors, qu’est-ce qui fait de ce théorème un « monument » ?
Ce n’est pas tant ce qu’il dit qui le rend si important, mais c’est aussi ce qu’il implique pour la physique fondamentale, et même pour la philosophie. Il montre en effet que les lois physiques émergent de quelque chose de plus profond, de plus fondamental : les symétries de l’Univers.
D’un point de vue philosophique, Emmy Noether nous dit ici que la nature aime l’harmonie, et que si l’univers que l’on observe semble si élégant, ce n’est pas un hasard, c’est inscrit dans son code mathématique.
Privatdozent
Lorsqu’elle revient à Göttingen en 1915, David Hilbert entend lui obtenir un poste de professeur. Malheureusement, les mentalités rétrogrades, soumises à une forte inertie, ne se mettent pas aisément en mouvement.
« Que penseront nos soldats, quand ils reviendront à l’université et verront qu’ils doivent apprendre aux pieds d’une femme ?
– Je ne vois pas pourquoi le sexe de la candidate serait un argument contre son admission comme Privatdozent. Après tout, nous sommes une université, pas des bains publics. »
David Hilbert, répondant à un professeur
Emmy donnera alors ses conférences en étant annoncée comme « David Hilbert » et devra en attendant des jours plus progressistes, se contenter d’un poste d’assistante. Elle devra attendre 1919 pour obtenir une habilitation à donner cours, et 1922 pour obtenir le titre de Privatdozent.
Ses conférences vont alors fédérer une communauté autour d’elle : les « Noether’s boys« , qui furent les vecteurs de ses travaux à travers l’Europe – notamment Bartel Van der Waerden, qui publiera – entre autre – les notes qu’il a prises au cours des conférences d’Emmy.
Consécration
En 1932, Emmy est invitée à donner une conférence plénière au congrès international des mathématiciens de Zurich.
La même année, elle reçoit avec son co-récipiendaire Emil Artin, le prix Alfred Ackermann-Teubner, accompagné de la somme de 60 000 Marks. Mais ce chapitre est tristement court…
Exil aux Etats-Unis
En 1933, Adolf Hitler devient chancelier. Emmy reçoit une lettre du Ministère des Sciences : elle se voit retirer le droit d’enseigner car elle est juive. Elle est expulsée de l’université.
Pendant un temps, elle recevra ses étudiants chez elle, pour continuer à donner cours, mais la montée du nazisme progresse et elle doit fuir.
Albert Einstein, qui avait déjà émigré aux États Unis, lui trouve un poste et la fait venir à Philapdelphie, à l’Université de Bryn Mawr. Son charisme et sa bienveillance vont attirer encore une fois foule d’étudiants à la suivre sur le campus pour assister à ses cours.

Ce répit sera toutefois de courte durée.
La plus grande…
En 1935, une tumeur bénigne et un kyste ovarien lui sont diagnostiqués. Malheureusement, durant l’intervention pourtant simple, des complications apparaissent. Elle n’y survivra pas et meurt quelques jours après, le 14 avril 1935, à seulement 53 ans.
Le monde scientifique sera alors plongé dans un deuil profond et se souviendra de la plus grande mathématicienne de tous les temps. Elle y aura toutefois laissé une empreinte indélébile.
« La plus grande mathématicienne qui a jamais vécu, et la plus grande femme scientifique vivante. »
Norbet Wiener
Et sa mémoire mérite de ne jamais disparaitre, surtout en ces temps troublés. #standupforscience

